RSA加解密流程-Easy to understand and humorous

RSA加密是一种非对称加密。可以在不直接传递密钥的情况下，完成解密；是由一对密钥来进行加解密的过程，分别称为公钥和私钥。
这一对密钥之间有数学相关，该加密算法的原理就是对一极大整数做因数分解的困难性来保证安全性。
通常个人保存私钥，公钥是公开的（可能同时多人持有）。

之前讲过 RSA 公钥加密算法，这里我们研究下原理。

RSA交互流程

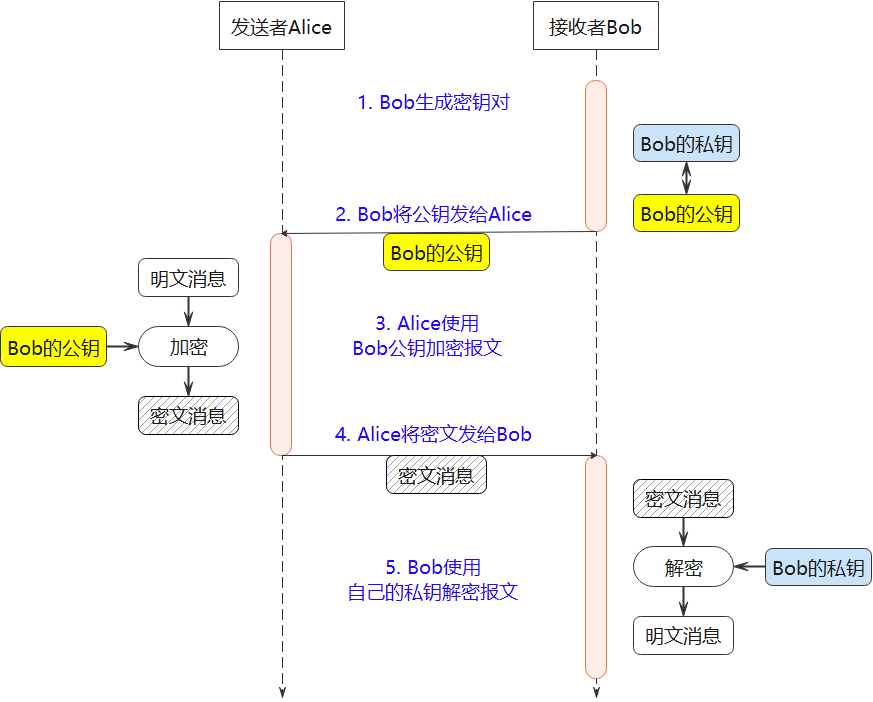
数论基础

一、素数

素数又称质数，指在一个大于1的自然数中，除了1和此整数自身外，不能被其他自然数整除的数。

二、模运算

模运算即求余运算。“模”是“Mod”的音译。和模运算紧密相关的一个概念是“同余”。数学上，当两个整数除以同一个正整数，若得相同余数，则二整数同余。

两个整数a，b，若它们除以正整数m所得的余数相等，则称a，b对于模m同余，记作: a ≡ b (mod m)；读作：a同余于b模m，或者，a与b关于模m同余。例如：26 ≡ 14 (mod 12)。

对于正整数p和整数a,b，取模运算：a mod p 表示a除以p的余数。
如果两个数a、b满足 a mod p = b mod p，则称他们模p相等，记做：a ≡ b (mod p)。

三、互质关系

如果两个正整数，除了1以外，没有其他公因子，我们就称这两个数是互质关系（coprime）。
比如，15和32没有公因子，所以它们是互质关系。这说明，不是质数也可以构成互质关系。

关于互质关系的结论：

任意两个质数构成互质关系，比如13和61。
一个数是质数，另一个数只要不是前者的倍数，两者就构成互质关系，比如3和10。
如果两个数之中，较大的那个数是质数，则两者构成互质关系，比如97和57。
1和任意一个自然数是都是互质关系，比如1和99。
p是大于1的整数，则p和p-1构成互质关系，比如57和56。
p是大于1的奇数，则p和p-2构成互质关系，比如17和15。

四、欧拉函数

tip 请思考以下问题

任意给定正整数n，请问在小于等于n的正整数之中，有多少个与n构成互质关系？
比如，在1到8之中，有多少个数与8构成互质关系？计算这个值的方法就叫做欧拉函数，以φ(n)表示。
在1到8之中，与8形成互质关系的是1、3、5、7，所以 φ(n) = 4。

φ(n)的计算

第一种情况
如果n=1，则 φ(1) = 1 。因为1与任何数（包括自身）都构成互质关系。

第二种情况
如果n是质数，则 φ(n)=n-1 。因为质数与小于它的每一个数，都构成互质关系。比如5与1、2、3、4都构成互质关系。

第三种情况
如果n是质数的某一个次方，即 n = p^k (p为质数，k为大于等于1的整数)，则 φ( p^k ) = p^k - p^{k-1} 。注意，此处为 p^(k-1) 哦。
比如 φ(8) = φ( 2^3 ) = 2^3 - 2^2 = 8 -4 = 4。

这是因为只有当一个数不包含质数p，才可能与n互质。而包含质数p的数一共有 p^{k-1}个。
上面的式子还可以写成下面的形式：

φ(p^k) = p^k - p^{k-1} = p^k (1 - \frac{1}{p})

可以看出，上面的第二种情况是 k=1 时的特例。

第四种情况
如果n可以分解成两个互质的整数之积，n = p1 × p2，则：φ(n) = φ(p1×p2) = φ(p1)φ(p2)

即积的欧拉函数等于各个因子的欧拉函数之积。比如，φ(56)=φ(8×7)=φ(8)×φ(7)=4×6=24。

这一条的证明要用到“中国剩余定理”。如果a与p1互质(a < p1)，b与p2互质(b < p2)，c与p1p2互质(c < p1p2)，则c与数对 (a,b) 是一一对应关系。由于a的值有φ(p1)种可能，b的值有φ(p2)种可能，则数对 (a,b) 有φ(p1)φ(p2)种可能，而c的值有φ(p1p2)种可能，所以φ(p1p2)就等于φ(p1)φ(p2)。

info 孙子定理

孙子定理是中国古代求解一次同余式组（见同余）的方法。是数论中一个重要定理。又称中国余数定理。
一元线性同余方程组问题最早可见于中国南北朝时期（公元5世纪）的数学著作《孙子算经》卷下第二十六题，
叫做“物不知数”问题，原文如下：

有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？即，一个整数除以三余二，除以五余三，除以七余二，求这个整数。《孙子算经》中首次提到了同余方程组问题，以及以上具体问题的解法，
因此在中文数学文献中也会将中国剩余定理称为孙子定理。

翻译过来就是有一个数除以三余二，除以五余三，除以七余二，问这个数是多少。

《孙子算经》解这道题目的“术文”和答案是：
“三三数之剩二，置一百四十；
五五数之剩三，置六十三；
七七数之剩二，置三十。
并之，得二百三十三，以二百十减之，即得。”“答曰：二十三。”

这些话是什么意思呢？用通俗的话来说，就是：
先求被3除余2，并能同时被5、7整除的数，这样的数最小是35；
再求被5除余3，并能同时被3、7整除的数，这样的数最小是63；
然后求被7除余2，并能同时被3、5整除的数，这样的数最小是30。
于是，由35+63+30=128，得到的128就是一个所要求得的数。但这个数并不是最小的。
再用求得的“128”减去或者加上3、5、7的最小公倍数“105”的倍数，就得到许许多多这样的数： {23，128，233，338，443，…}
从而可知，23、128、233、338、443、…等都是这一道题目的解，而其中最小的解是23。

第五种情况
因为任意一个大于1的正整数，都可以写成一系列质数的积。

n = p_1^{k1}p_2^{k2}...p_r^{kr}

根据第4条的结论，得到:

φ(n) = φ(p_1^{k1})φ(p_2^{k2})...φ(p_r^{kr})

再根据第3条的结论，得到:

φ(n) = p_1^{k1}p_2^{k2}...p_r^{kr}(1 - \frac{1}{p_1})(1 - \frac{1}{p_2})...(1 - \frac{1}{p_r})

也就等于:

φ(n) = n(1 - \frac{1}{p_1})(1 - \frac{1}{p_2})...(1 - \frac{1}{p_r})

这就是欧拉函数的通用计算公式。
比如，1323 的欧拉函数，计算过程如下：

φ(1323) = φ(3^3*7^2) = 1323(1 - \frac{1}{3})(1 - \frac{1}{7}) = 756

五、欧拉定理

欧拉定理是RSA算法的核心。

欧拉定理指的是：如果两个正整数a和n互质，则n的欧拉函数 φ(n) 可以让下面的等式成立:

a^{φ(n)} ≡ 1 (mod n)

。

也就是说，a的φ(n)次方被n除的余数为1。或者说，a的φ(n)次方减去1，可以被n整除。
比如，3和7互质，而7的欧拉函数φ(7)等于6，所以3的6次方（729）减去1，可以被7整除（728/7=104）。

欧拉定理可以大大简化某些运算。
比如，7和10互质，根据欧拉定理，

7^{φ(10)} ≡ 1 (mod 10)

。
已知 φ(10) 等于4，所以马上得到7的4倍数次方的个位数肯定是1。

7^{4k} ≡ 1 (mod 10)

。
因此，7的任意次方的个位数(例如7的222次方)。

欧拉定理有一个特殊情况
假设正整数a与质数p互质，因为质数p的φ(p)等于p-1，则欧拉定理可以写成

a^{p-1} ≡ 1 (mod p)

。

这就是著名的费马小定理。它是欧拉定理的特例。

六、模反元素

如果两个正整数a和n互质，那么一定可以找到整数b，使得ab-1被n整除，或者说ab被n除的余数是1。
ab ≡ 1 (mod n), 这时，b就叫做a的模反元素。

比如，3和11互质，那么3的模反元素就是4，因为 (3 × 4)-1 可以被11整除。
显然，模反元素不止一个， 4加减11的整数倍都是3的模反元素 {…,-18,-7,4,15,26,…}，即如果b是a的模反元素，则 b+kn 都是a的模反元素。

欧拉定理可以用来证明模反元素必然存在。

a^{φ(n)} = a * a^{φ(n)-1} ≡ 1 (mod n)

可以看到，a的 φ(n)-1 次方，就是a的模反元素。

RSA已知高位攻击

RSA已知高位攻击是一种利用已知部分密钥高位信息来破解RSA加密的方法。此攻击基于Coppersmith定理，该定理表明在已知部分高位比特的情况下，可以在多项式时间内分解大整数N。

Coppersmith定理指出，如果已知大整数N的部分高位比特，并且这些比特的数量满足一定条件，则可以在多项式时间内分解N。
例如，如果已知N的高位1/5比特，可以在logN时间内分解N。

以下是一个示例代码，展示了如何利用已知高位信息来破解RSA加密:
首先定义已知参数，包括大整数N和p的高位。然后，计算p的低位，并构造一个多项式来求解p的完整值。
最后，通过分解N来获取p和q。

from sage.all import *

# 已知参数
n = 0x... # 大整数N
p_high = 0x... # 已知的p的高位
e = 0x10001 # 公钥指数

# 计算p的低位
kbits = n.nbits() - p_high.nbits()
p_high <<= kbits

# 构造多项式并求解
PR.<x> = PolynomialRing(Zmod(n))
f = x + p_high
roots = f.small_roots(X=2^kbits, beta=0.4)

# 获取p和q
if roots:
    p = p_high + int(roots[0])
    q = n // p
    print(f"p: {p}")
    print(f"q: {q}")

目录CONTENT

RSA加解密流程