国密SM4
SM4国密算法是一种对称密码算法,也称为SM4分组密码算法,它在中国国家密码管理局发布的国家密码算法标准中被广泛采用。
SM4 为无线局域网标准的分组加密算法,对称加密,用于替代 DES/AES 等国际算法, SM4 算法与 AES 算法具有相同的密钥长度和分组长度,均为 128 位,故对消息进行加解密时,若消息长度过长,需要进行分组,要消息长度不足,则要进行填充。
SM4 是一个分组算法,分组长度和密钥长度均为128比特,加密算法与密钥扩展算法都采用32轮非线性迭代结构,解密算法与加密算法的结构相同,只是轮密钥的使用顺序相反,解密轮密钥是加密轮密钥的逆序。 最初作为无线局域网专用密码算法发布,后成为分组密码算法行业标准。
目前支持SMS4算法的产品已达700余款,覆盖了各种有对称加密需求的应用。 由于SMS4算法最初用于无线局域网芯片WAPI协议中,支持SMS4算法的WAPI无线局域网芯片已超过350多个型号,全球累计出货量超过70亿颗。 在金融领域,仅统计支持SMS4算法的智能密码钥匙出货量已超过1.5亿支。
此外,SMS4算法已被纳人可信计算组织(TCG)发布的可信平台模块库规范(TPIM2.0)中。
SM4 VS DES VS AES
| SM4 | DES | AES | |
|---|---|---|---|
| 计算轮数 | 32 | 16(3DES 为 16*3) | 10/12/14 |
| 密码部件 | S 盒、非线性变换、线性变换、合成变换 | 标准算术和逻辑运算、先替换后置换,不含线性变换 | S 盒、行移位变换、列混合变换、圈密钥加变换(AddRoundKey) |
运算操作
国密SM4包含的运算操作主要有:异或运算、移位变换、盒变换...
异或运算 XOR
异或运算(XOR)是 exclusive OR 的缩写。英语的 exclusive 意思是"专有的,独有的", 可以理解为 XOR 是更单纯的 OR 运算。
XOR 主要用来判断两个值是否不同。 在异或运算中,如果参与运算的两个值相同,则结果为假(或0);如果两个值不同,则结果为真
如果约定0 为 false,1 为 true,那么 XOR 的运算真值表如下:
| A | B | A XOR B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
XOR 一般使用插入符号(caret)^表示。上述运算真值表可以表达为:
0 ^ 0 = 0
0 ^ 1 = 1
1 ^ 0 = 1
1 ^ 1 = 0
移位变换
在密码学中,移位是一种简单的加密技术, 通过将字母或数字按照固定的位数进行移动来加密文本。

盒变换
盒变换是一种非线性变换,它通过查找预定义的S盒(Substitution Box)来替换输入的每个字节。 S盒是一个固定的字节替代表,将输入字节映射到输出字节。
在SM4中,S盒是一个16x16的矩阵,包含了固定的字节替代值。 盒变换可以增加加密算法的非线性和安全性。
SM4盒变换矩阵如图所示: 
SM4 加/解密
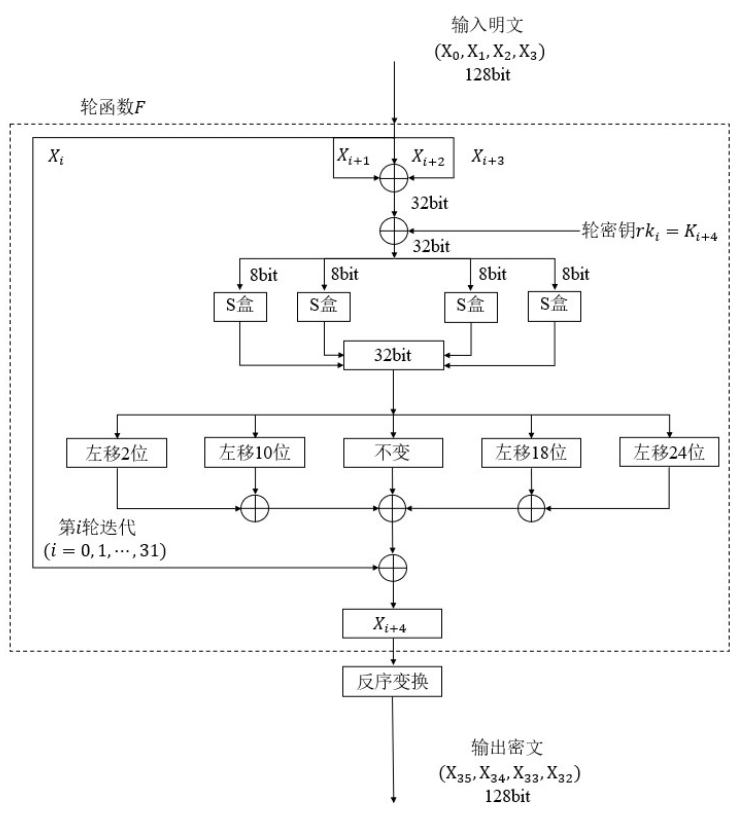
如上图SM4算法的加/解密流程图。输入为128bit的明文数据,输出为128bit的密文数据。 整个加/解密过程,需要经过32( i = 0 , 1 , . . . , 31 ) (i=0,1,...,31)(i=0,1,...,31)轮迭代, 当i=0时进行第一轮变换,一直进行到i = 31结束。加/解过程表示为,其中F为轮函数,即32轮非线性迭代机制。
将输入的128bit的明文,按bit位分成4组32bit的数据,表示为( Xi , Xi+1 , Xi+2 , Xi+3), 其中Xi(i=0,1,…,31)为32bit明文数据。
首先,将Xi保持不变,将Xi+1 , Xi+2 , Xi+3和轮密钥rki异或得到一个32bit的数据, 作为盒变换的输入,表示为sboxinput=Xi+1⊕Xi+2⊕Xi+3⊕rki,其中 ⊕ 表示异或运算,irki为轮密钥。
然后,将 sboxinput拆分成4个8bit的数据,分别执行盒变换操作。将4个盒变换的输出(每个输出依然为8bit)组合成一个32bit的 sboxoutput。
然后,将这个32bit的 sboxoutput 执行移位变换操作。执行4次循环左移操作,分别循环左移2,10,18,24位,得到4个32bit的结果,分别记为y2, y10, y18, y24。
将移位的结果 y2, y10, y18, y24,盒变换的输出 sboxoutput,第一组输入明文Xi,三者进行异或,得到Xi+4, 表示为Xi+4 = sboxoutput ⊕ y2 ⊕ y10 ⊕ y18 ⊕ y24 ⊕ Xi。
实际加/解密过程中,上述流程共执行32轮,每一轮使用都使用不同的轮密钥 rki = Ki+4(i=0,1,…,31),轮密钥通过密钥扩展产生。将轮函数F最后生成的4个32bit数据 X32, X33, X34, X34 合并后执行反序变换操作,得到最终的128bit的密文数据,即X35 , X34 , X33 , X32。
SM4 密钥扩展
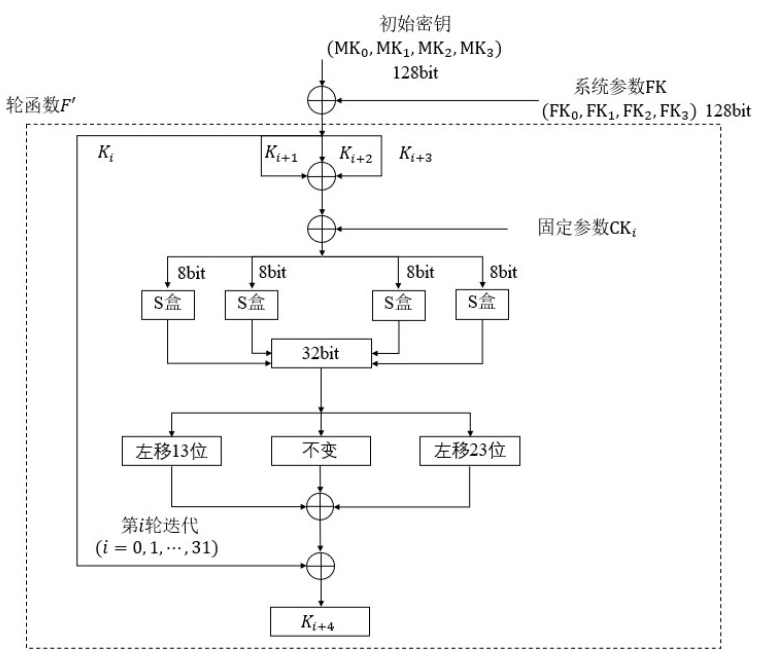
密钥扩展流程图如上图所示。输入为初始密钥,是一个128bit的数据,输出为32bit的轮密钥。
首先,将初始密钥按位拆分为4个32bit的数据,记为 MK0 , MK1 , MK2 , MK3。然后将初始密钥与系统参数FK,进行按位异或,得到用于循环的密钥 K0 , K1 , K2 , K3,其中 K0 = MK0 ⊕ FK0 , K1 = K1 ⊕ FK1 , K2 = K2 ⊕ FK2 , K3 = K3 ⊕ FK3。
SM4加解密代码样例
Java 代码
需要注意的是,此处仅是SM4的简单实现。而实际运用的时候,还需考虑各种工作模式(例如 OFB 或是 CFB)以及输入分组长度不是 128bit 的整数倍时需要添加的填充(例如 PKCS #7)。
此处的代码仅用于展示 SM4 加解密过程的原理,输入的加密数据长度仅支持 128bit(长度为 16 的 byte 数组)
public class SM4 {
int[] key_r;
/* 初始化轮密钥 */
SM4(byte[] key) {
this.key_r = keyGenerate(key);
}
/* 加密 */
public byte[] encrypt(byte[] plaintext) {
return sm4Main(plaintext, key_r, 0);
}
/* 解密 */
public byte[] decrypt(byte[] ciphertext) {
return sm4Main(ciphertext, key_r, 1);
}
/* 密钥拓展 */
private int[] keyGenerate(byte[] key) {
int[] key_r = new int[32];//轮密钥rk_i
int[] key_temp = new int[4];
int box_in, box_out;//盒变换输入输出
final int[] FK = {0xa3b1bac6, 0x56aa3350, 0x677d9197, 0xb27022dc};
final int[] CK = {
0x00070e15, 0x1c232a31, 0x383f464d, 0x545b6269,
0x70777e85, 0x8c939aa1, 0xa8afb6bd, 0xc4cbd2d9,
0xe0e7eef5, 0xfc030a11, 0x181f262d, 0x343b4249,
0x50575e65, 0x6c737a81, 0x888f969d, 0xa4abb2b9,
0xc0c7ced5, 0xdce3eaf1, 0xf8ff060d, 0x141b2229,
0x30373e45, 0x4c535a61, 0x686f767d, 0x848b9299,
0xa0a7aeb5, 0xbcc3cad1, 0xd8dfe6ed, 0xf4fb0209,
0x10171e25, 0x2c333a41, 0x484f565d, 0x646b7279
};
//将输入的密钥每32比特合并,并异或FK
for (int i = 0; i < 4; i++) {
key_temp[i] = jointBytes(key[4 * i], key[4 * i + 1], key[4 * i + 2], key[4 * i + 3]);
key_temp[i] = key_temp[i] ^ FK[i];
}
//32轮密钥拓展
for (int i = 0; i < 32; i++) {
box_in = key_temp[1] ^ key_temp[2] ^ key_temp[3] ^ CK[i];
box_out = sBox(box_in);
key_r[i] = key_temp[0] ^ box_out ^ shift(box_out, 13) ^ shift(box_out, 23);
key_temp[0] = key_temp[1];
key_temp[1] = key_temp[2];
key_temp[2] = key_temp[3];
key_temp[3] = key_r[i];
}
return key_r;
}
/* 加解密主函数 */
private static byte[] sm4Main(byte[] input, int[] key_r, int mod) {
int[] text = new int[4];//32比特字
//将输入以32比特分组
for (int i = 0; i < 4; i++) {
text[i] = jointBytes(input[4 * i], input[4 * i + 1], input[4 * i + 2], input[4 * i + 3]);
}
int box_input, box_output;//盒变换输入和输出
for (int i = 0; i < 32; i++) {
int index = (mod == 0) ? i : (31 - i);//通过改变key_r的顺序改变模式
box_input = text[1] ^ text[2] ^ text[3] ^ key_r[index];
box_output = sBox(box_input);
int temp = text[0] ^ box_output ^ shift(box_output, 2) ^ shift(box_output, 10) ^ shift(box_output, 18) ^ shift(box_output, 24);
text[0] = text[1];
text[1] = text[2];
text[2] = text[3];
text[3] = temp;
}
byte[] output = new byte[16];//输出
//将结果的32比特字拆分
for (int i = 0; i < 4; i++) {
System.arraycopy(splitInt(text[3 - i]), 0, output, 4 * i, 4);
}
return output;
}
/* 将32比特数拆分成4个8比特数 */
private static byte[] splitInt(int n) {
return new byte[]{(byte) (n >>> 24), (byte) (n >>> 16), (byte) (n >>> 8), (byte) n};
}
/* 将4个8比特数合并成32比特数 */
private static int jointBytes(byte byte_0, byte byte_1, byte byte_2, byte byte_3) {
return ((byte_0 & 0xFF) << 24) | ((byte_1 & 0xFF) << 16) | ((byte_2 & 0xFF) << 8) | (byte_3 & 0xFF);
}
/* S盒变换 */
private static int sBox(int box_input) {
//s盒的参数
final int[] SBOX = {
0xD6, 0x90, 0xE9, 0xFE, 0xCC, 0xE1, 0x3D, 0xB7, 0x16, 0xB6, 0x14, 0xC2, 0x28, 0xFB, 0x2C, 0x05, 0x2B, 0x67, 0x9A,
0x76, 0x2A, 0xBE, 0x04, 0xC3, 0xAA, 0x44, 0x13, 0x26, 0x49, 0x86, 0x06, 0x99, 0x9C, 0x42, 0x50, 0xF4, 0x91, 0xEF,
0x98, 0x7A, 0x33, 0x54, 0x0B, 0x43, 0xED, 0xCF, 0xAC, 0x62, 0xE4, 0xB3, 0x1C, 0xA9, 0xC9, 0x08, 0xE8, 0x95, 0x80,
0xDF, 0x94, 0xFA, 0x75, 0x8F, 0x3F, 0xA6, 0x47, 0x07, 0xA7, 0xFC, 0xF3, 0x73, 0x17, 0xBA, 0x83, 0x59, 0x3C, 0x19,
0xE6, 0x85, 0x4F, 0xA8, 0x68, 0x6B, 0x81, 0xB2, 0x71, 0x64, 0xDA, 0x8B, 0xF8, 0xEB, 0x0F, 0x4B, 0x70, 0x56, 0x9D,
0x35, 0x1E, 0x24, 0x0E, 0x5E, 0x63, 0x58, 0xD1, 0xA2, 0x25, 0x22, 0x7C, 0x3B, 0x01, 0x21, 0x78, 0x87, 0xD4, 0x00,
0x46, 0x57, 0x9F, 0xD3, 0x27, 0x52, 0x4C, 0x36, 0x02, 0xE7, 0xA0, 0xC4, 0xC8, 0x9E, 0xEA, 0xBF, 0x8A, 0xD2, 0x40,
0xC7, 0x38, 0xB5, 0xA3, 0xF7, 0xF2, 0xCE, 0xF9, 0x61, 0x15, 0xA1, 0xE0, 0xAE, 0x5D, 0xA4, 0x9B, 0x34, 0x1A, 0x55,
0xAD, 0x93, 0x32, 0x30, 0xF5, 0x8C, 0xB1, 0xE3, 0x1D, 0xF6, 0xE2, 0x2E, 0x82, 0x66, 0xCA, 0x60, 0xC0, 0x29, 0x23,
0xAB, 0x0D, 0x53, 0x4E, 0x6F, 0xD5, 0xDB, 0x37, 0x45, 0xDE, 0xFD, 0x8E, 0x2F, 0x03, 0xFF, 0x6A, 0x72, 0x6D, 0x6C,
0x5B, 0x51, 0x8D, 0x1B, 0xAF, 0x92, 0xBB, 0xDD, 0xBC, 0x7F, 0x11, 0xD9, 0x5C, 0x41, 0x1F, 0x10, 0x5A, 0xD8, 0x0A,
0xC1, 0x31, 0x88, 0xA5, 0xCD, 0x7B, 0xBD, 0x2D, 0x74, 0xD0, 0x12, 0xB8, 0xE5, 0xB4, 0xB0, 0x89, 0x69, 0x97, 0x4A,
0x0C, 0x96, 0x77, 0x7E, 0x65, 0xB9, 0xF1, 0x09, 0xC5, 0x6E, 0xC6, 0x84, 0x18, 0xF0, 0x7D, 0xEC, 0x3A, 0xDC, 0x4D,
0x20, 0x79, 0xEE, 0x5F, 0x3E, 0xD7, 0xCB, 0x39, 0x48
};
byte[] temp = splitInt(box_input);//拆分32比特数
byte[] output = new byte[4];//单个盒变换输出
//盒变换
for (int i = 0; i < 4; i++) {
output[i] = (byte) SBOX[temp[i] & 0xFF];
}
//将4个8位字节合并为一个字作为盒变换输出
return jointBytes(output[0], output[1], output[2], output[3]);
}
/* 循环移位: 将input左移n位 */
private static int shift(int input, int n) {
return (input >>> (32 - n)) | (input << n);
}
}
代码走读-循环移位
>> 算数右移, 是将 2 进制数整体右移一位,原先最低位舍弃,变为原先的次低位,最高位与原先最高位相同,效果类似于除 2。 >>> 无符号右移,是将 2 进制数整体右移一位,原先最低位舍弃,变为原先的次低位,最高位补 0。
/* 循环移位: 将input左移n位 */
private static int shift(int input, int n) {
return (input >>> (32 - n)) | (input << n);
}
将一个 32bit 数拆分成 4 个 8bit 数
/* 将32比特数拆分成4个8比特数 */
private static byte[] splitInt(int n) {
return new byte[]{(byte) (n >>> 24), (byte) (n >>> 16), (byte) (n >>> 8), (byte) n};
}
将 4 个 8bit 数合并为 1 个 32bit 数
此方法的是把 4 个 8bit 数合并为 1 个 32bit 数,输入 4 个 byte 类型,输出一个 int 类型。
/* 将4个8比特数合并成32比特数 */
private static int jointBytes(byte byte_0, byte byte_1, byte byte_2, byte byte_3) {
return ((byte_0 & 0xFF) << 24) | ((byte_1 & 0xFF) << 16) | ((byte_2 & 0xFF) << 8) | (byte_3 & 0xFF);
}
需要注意的是,因为 byte 类型存在符号位,对于 byte 的左移操作,倘若 byte 为负数,那么左移结果和我们想象的会不太一样。
例如我们希望 0xFF 左移 8 位的结果为 0x0000FF00,但实际上结果却是 0xFFFFFF00。
byte b = (byte)0xFF;
System.out.printf("%08x", b<<8); //0xffffff00
这是因为在 byte 类型左移时,会先转化成 int 类型,但由于符号位的原因,0xFF 会被转化成 0xFFFFFFFF(扩大的部分用符号位填充),导致结果与预期不同。
为了抵消掉符号位的影响,我们可以先与上 0xFF。 在进行与运算时,byte 类型同样会先转化成 int 类型,但我们只取其最低的 8 位,其余位置 0,便可抵消符号位的影响。
代码走读-盒变换
S 盒实际上是一个 8 比特到 8 比特的映射。
S 盒为 16×16 的表格,输入的 8 比特数的前 4 比特确定行,后 4 比特确定列,行和列共同确定表格中的一项
下表是盒变换对应的表格:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | a | b | c | d | e | f | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0xd6 | 0x90 | 0xe9 | 0xfe | 0xcc | 0xe | 0x3d | 0xb7 | 0x16 | 0xb | 0x14 | 0xc2 | 0x28 | 0xfb | 0x2c | 0x05 |
| 1 | 0x2b | 0x67 | 0x9a | 0x76 | 0x2a | 0xb | 0x04 | 0xc3 | 0xaa | 0x4 | 0x13 | 0x26 | 0x49 | 0x86 | 0x06 | 0x99 |
| 2 | 0x9c | 0x42 | 0x50 | 0xf4 | 0x91 | 0xe | 0x98 | 0x7a | 0x33 | 0x5 | 0x0b | 0x43 | 0xed | 0xcf | 0xac | 0x62 |
| 3 | 0xe4 | 0xb3 | 0x1c | 0xa9 | 0xc9 | 0x0 | 0xe8 | 0x95 | 0x80 | 0xd | 0x94 | 0xfa | 0x75 | 0x8f | 0x3f | 0xa6 |
| 4 | 0x47 | 0x07 | 0xa7 | 0xfc | 0xf3 | 0x7 | 0x17 | 0xba | 0x83 | 0x5 | 0x3c | 0x19 | 0xe6 | 0x85 | 0x4f | 0xa8 |
| 5 | 0x68 | 0x6b | 0x81 | 0xb2 | 0x71 | 0x6 | 0xda | 0x8b | 0xf8 | 0xe | 0x0f | 0x4b | 0x70 | 0x56 | 0x9d | 0x35 |
| 6 | 0x1e | 0x24 | 0x0e | 0x5e | 0x63 | 0x5 | 0xd1 | 0xa2 | 0x25 | 0x2 | 0x7c | 0x3b | 0x01 | 0x21 | 0x78 | 0x87 |
| 7 | 0xd4 | 0x00 | 0x46 | 0x57 | 0x9f | 0xd | 0x27 | 0x52 | 0x4c | 0x3 | 0x02 | 0xe7 | 0xa0 | 0xc4 | 0xc8 | 0x9e |
| 8 | 0xea | 0xbf | 0x8a | 0xd2 | 0x40 | 0xc | 0x38 | 0xb5 | 0xa3 | 0xf | 0xf2 | 0xce | 0xf9 | 0x61 | 0x15 | 0xa1 |
| 9 | 0xe0 | 0xae | 0x5d | 0xa4 | 0x9b | 0x3 | 0x1a | 0x55 | 0xad | 0x9 | 0x32 | 0x30 | 0xf5 | 0x8c | 0xb1 | 0xe3 |
| a | 0x1d | 0xf6 | 0xe2 | 0x2e | 0x82 | 0x6 | 0xca | 0x60 | 0xc0 | 0x2 | 0x23 | 0xab | 0x0d | 0x53 | 0x4e | 0x6f |
| b | 0xd5 | 0xdb | 0x37 | 0x45 | 0xde | 0xf | 0x8e | 0x2f | 0x03 | 0xf | 0x6a | 0x72 | 0x6d | 0x6c | 0x5b | 0x51 |
| c | 0x8d | 0x1b | 0xaf | 0x92 | 0xbb | 0xd | 0xbc | 0x7f | 0x11 | 0xd | 0x5c | 0x41 | 0x1f | 0x10 | 0x5a | 0xd8 |
| d | 0x0a | 0xc1 | 0x31 | 0x88 | 0xa5 | 0xc | 0x7b | 0xbd | 0x2d | 0x7 | 0xd0 | 0x12 | 0xb8 | 0xe5 | 0xb4 | 0xb0 |
| e | 0x89 | 0x69 | 0x97 | 0x4a | 0x0c | 0x9 | 0x77 | 0x7e | 0x65 | 0xb | 0xf1 | 0x09 | 0xc5 | 0x6e | 0xc6 | 0x84 |
| f | 0x18 | 0xf0 | 0x7d | 0xec | 0x3a | 0xd | 0x4d | 0x20 | 0x79 | 0xe | 0x5f | 0x3e | 0xd7 | 0xcb | 0x39 | 0x48 |
例如 sbox(13)=0x76, sbox(36)=0xe8
实际上,我们并不需要特地将 S盒 设置成 16×16 的二维数组,可以直接设置成长度为 256 的一维数组,就不需要拆分 8 比特确定行和列了。 该一维数组可以参考上述代码中的 final int[] SBOX = {...} 定义。
代码走读-加解密主函数
这个函数输入的是 byte 数组,输出也是 byte 数组。
byte 只有 8 位,而加解密过程我们是以 32bit,即 int 类型为单位运算的,故先要把 byte 数组合并成 int 数组
最后函数输出的是 byte 类型数组,同样的,需要把最后 int 类型的结果转化成 byte。
其他的实现方式
当然还有其他更加简洁的实现方式。 比如 bouncycastle 的实现。
maven 依赖
<dependency>
<groupId>org.bouncycastle</groupId>
<artifactId>bcprov-jdk15on</artifactId>
<version>1.59</version>
</dependency>
import com.github.houbb.secret.api.exception.SecretRuntimeException;
import org.bouncycastle.jce.provider.BouncyCastleProvider;
import org.bouncycastle.pqc.math.linearalgebra.ByteUtils;
import javax.crypto.Cipher;
import javax.crypto.spec.SecretKeySpec;
import java.security.Key;
import java.security.Security;
import java.util.Arrays;
/**
* Sm4 国密算法
*/
public final class Sm4Util {
private Sm4Util() {
}
static {
Security.addProvider(new BouncyCastleProvider());
}
private static final String ENCODING = "UTF-8";
private static final String ALGORITHM_NAME = "SM4";
/**
* PKCS5Padding NoPadding 补位规则,PKCS5Padding缺位补0,NoPadding不补
*/
private static final String ALGORITHM_NAME_ECB_PADDING = "SM4/ECB/PKCS5Padding";
/**
* ECB加密模式,无向量
* @param algorithmName 算法名称
* @param mode 模式
* @param key key
* @return 结果
*/
private static Cipher generateEcbCipher(String algorithmName, int mode, byte[] key) throws Exception {
Cipher cipher = Cipher.getInstance(algorithmName, BouncyCastleProvider.PROVIDER_NAME);
Key sm4Key = new SecretKeySpec(key, ALGORITHM_NAME);
cipher.init(mode, sm4Key);
return cipher;
}
/**
* sm4加密
* 加密模式:ECB 密文长度不固定,会随着被加密字符串长度的变化而变化
*
* @param hexKey 16进制密钥(忽略大小写)
* @param plainText 待加密字符串
* @return 返回16进制的加密字符串
* @since 0.0.5
*/
public static String encryptEcb(String hexKey, String plainText) {
try {
String cipherText = "";
// 16进制字符串-->byte[]
byte[] keyData = ByteUtils.fromHexString(hexKey);
// String-->byte[]
//当加密数据为16进制字符串时使用这行
byte[] srcData = plainText.getBytes(ENCODING);
// 加密后的数组
byte[] cipherArray = encryptEcbPadding(keyData, srcData);
// byte[]-->hexString
cipherText = ByteUtils.toHexString(cipherArray);
return cipherText;
} catch (Exception exception) {
throw new SecretRuntimeException(exception);
}
}
/**
* 加密模式之Ecb
*
* @param key 秘钥
* @param data 待加密的数据
* @return 字节数组
* @since 0.0.5
*/
public static byte[] encryptEcbPadding(byte[] key, byte[] data) {
try {
//声称Ecb暗号,通过第二个参数判断加密还是解密
Cipher cipher = generateEcbCipher(ALGORITHM_NAME_ECB_PADDING, Cipher.ENCRYPT_MODE, key);
return cipher.doFinal(data);
} catch (Exception exception) {
throw new SecretRuntimeException(exception);
}
}
//解密****************************************
/**
* sm4解密
*
* 解密模式:采用ECB
* @param hexKey 16进制密钥
* @param cipherText 16进制的加密字符串(忽略大小写)
* @return 解密后的字符串
* @since 0.0.5
*/
public static String decryptEcb(String hexKey, String cipherText) {
try {
// 用于接收解密后的字符串
String decryptStr = "";
// hexString-->byte[]
byte[] keyData = ByteUtils.fromHexString(hexKey);
// hexString-->byte[]
byte[] cipherData = ByteUtils.fromHexString(cipherText);
// 解密
byte[] srcData = decryptEcbPadding(keyData, cipherData);
// byte[]-->String
decryptStr = new String(srcData, ENCODING);
return decryptStr;
} catch (Exception exception) {
throw new SecretRuntimeException(exception);
}
}
/**
* 解密
*
* @param key 秘钥
* @param cipherText 密文
* @return 结果
* @since 0.0.5
*/
public static byte[] decryptEcbPadding(byte[] key, byte[] cipherText) {
try {
//生成Ecb暗号,通过第二个参数判断加密还是解密
Cipher cipher = generateEcbCipher(ALGORITHM_NAME_ECB_PADDING, Cipher.DECRYPT_MODE, key);
return cipher.doFinal(cipherText);
} catch (Exception exception) {
throw new SecretRuntimeException(exception);
}
}
/**
* 验证数据
* @param hexKey key
* @param cipherText 密文
* @param plainText 明文
* @return 结果
* @since 0.0.5
*/
public static boolean verifyEcb(String hexKey, String cipherText, String plainText) {
try {
// 用于接收校验结果
boolean flag = false;
// hexString-->byte[]
byte[] keyData = ByteUtils.fromHexString(hexKey);
// 将16进制字符串转换成数组
byte[] cipherData = ByteUtils.fromHexString(cipherText);
// 解密
byte[] decryptData = decryptEcbPadding(keyData, cipherData);
// 将原字符串转换成byte[]
byte[] srcData = plainText.getBytes(ENCODING);
// 判断2个数组是否一致
flag = Arrays.equals(decryptData, srcData);
return flag;
} catch (Exception exception) {
throw new SecretRuntimeException(exception);
}
}
}


评论区